taylor series error calculator
Notice the interval of convergence. To have an approximation accurate to within 105 we choose nlarge enough to have e n1.
Cochranmath Error Analysis Of Taylor Series
In this video we use Taylors inequality to estimate the expected error in using a Taylor Polynomial to estimate a function value.

. Evaluate the remainder by changing the value of x. Purpose of use academic assignment CommentRequest huh i was using this to check an assignment using a taylor series approximation and i think i found a misprint in my textbooks function when i checked it against this and another sources taylor series approximation. F x. If you want the Maclaurin polynomial just set the point to.
JoeFoster The Taylor Remainder TaylorsFormula. Compute the n 1 th n1textth n 1 th derivative of f x. Using 2nd order Taylor series. Taylor series are used to estimate the value of functions at least theoretically - now days we can usually use the calculator or computer to calculate directly Graph function sin x and its 5 th order Taylor Polynomial centered at 0.
E x n 0 1 n x n n. So in this case weve got general formulas so all we need to do is plug these into the Taylor Series formula and be done with the problem. ERROR ESTIMATES IN TAYLOR APPROXIMATIONS Suppose we approximate a function fx near x a by its Taylor polyno-mial T nxHow accurate is the approximation. Ex ˇ1 x gives a better fit.
Equation B411 is called the Taylor series or Taylors formula. By using this website you agree to our Cookie Policy. A Taylor polynomial approximates the value of a function and in many cases its helpful to measure the accuracy of an approximation. Taylor Polynomial Approximation of a Continuous Function.
Free TaylorMaclaurin Series calculator - Find the TaylorMaclaurin series representation of functions step-by-step This website uses cookies to ensure you get the best experience. Around the Point a default a 0 Maximum Power of the Expansion. SolveMyMaths Taylor Series Expansion Calculator. 105 which is true if n8.
A Taylor Maclaurin polynomial is a polynomial that results from truncating a Taylor Maclaurin power series to a specified degree. You can specify the order of the Taylor polynomial. Input the function you want to expand in Taylor serie. This result is an immediate consequence of the Lagrange remainder of and.
In essence the theorem states that any smooth function can be ap-proximated as a polynomial. Taylor approximation is local Approximate ex using c -1. Therefore the Taylor series for fx sinxcentered at a 0 converges and further as we hoped and expected we now know that it converges to sinxfor all x. Where f n a is the nth order derivative of function f x as evaluated at x a n is the order and a is where the series is centered.
A Taylor series provides us a polynomial approximation of a function centered around point a. The Maclaurin series is just a Taylor series centered at a 0. Change the function definition 2. A calculator for finding the expansion and form of the Taylor Series of a given function.
Fx Tnx Rnx Notice that the addition of the remainder term Rnx turns the approximation into an equation. Follow the prescribed steps. The formula used by taylor series calculator for calculating a series for a function is given as. Ex ˇ1 does not give a good fit.
Indeed if is any function which satisfies the hypotheses of Taylors theorem and for which there exists a real number satisfying on some interval the remainder satisfies on the same interval. The coefficient dfracfx-fax-a of x-a is the average slope of ft as t moves from ta to txtext We can picture this as the. The previous solution wasnt too bad and we often have to do things in that manner. 1 importnumpy as np 2 x 20 3 pn 00 4 forkinrange15.
Taylor and Maclaurin Power Series Calculator. For the error epn1 1 n1. Taylor Series Calculator with Steps Taylor Series Laurent Series Maclaurin Series. The calculator will find the Taylor or power series expansion of the given function around the given point with steps shown.
We can define the polynomial this way. Heres the formula for. X a k. How to Input.
Iffx hasderivativesofallordersinanopenintervalIcontainingathenforeachpositiveinteger nandforeachxI fx. Because the behavior of polynomials can be easier to understand than functions such as sinx we can use a Taylor series to help in solving differential equations infinite sums and advanced physics problems. In fact ep81 e 9. Epn1 e n1.
E x n 0 1 n x n n. If the remainder is omitted the right side of Eq. Using 0th order Taylor series. F x n 0 f k a k.
To find the Maclaurin Series simply set your Point to zero 0. This information is provided by the Taylor remainder term. 5aFind the Taylor Series directly using the formula for Taylor Series for fx lnx1 centered at a 0. Taylors inequality is an estimate result for the value of the remainder term in any -term finite Taylor series approximation.
The th-degree Taylor polynomial of a function at is the polynomial formed by using terms of the Taylor series representation of the function. Ecx 0 cx1 To bound the error we have e0 ecxe1 1 n1. B411 is the Taylor polynomial approximation to f x. 5 pn xk mathfactorialk 6 err npexp20 - pn 6.
Added Nov 4 2011 by sceadwe in Mathematics. Set the order of the Taylor polynomial 3. Ex ˇ1 x x22 gives a a really good fit. Enter a the centre of the Series and fx the function.
Using 1st order Taylor series.

Taylor Series With Max Bound On Error Of Logarithmic Function Youtube

Find The Error Bound For A Taylor Polynomial Youtube

Ap Calculus Bc Review Lagrange Error Bound Magoosh Blog High School

Taylor S Remainder Theorem Youtube

Solved 1 The Taylor Series Of Sin X Is Given By 3 Sin X Chegg Com

Proof Of The Lagrange Error Estimate
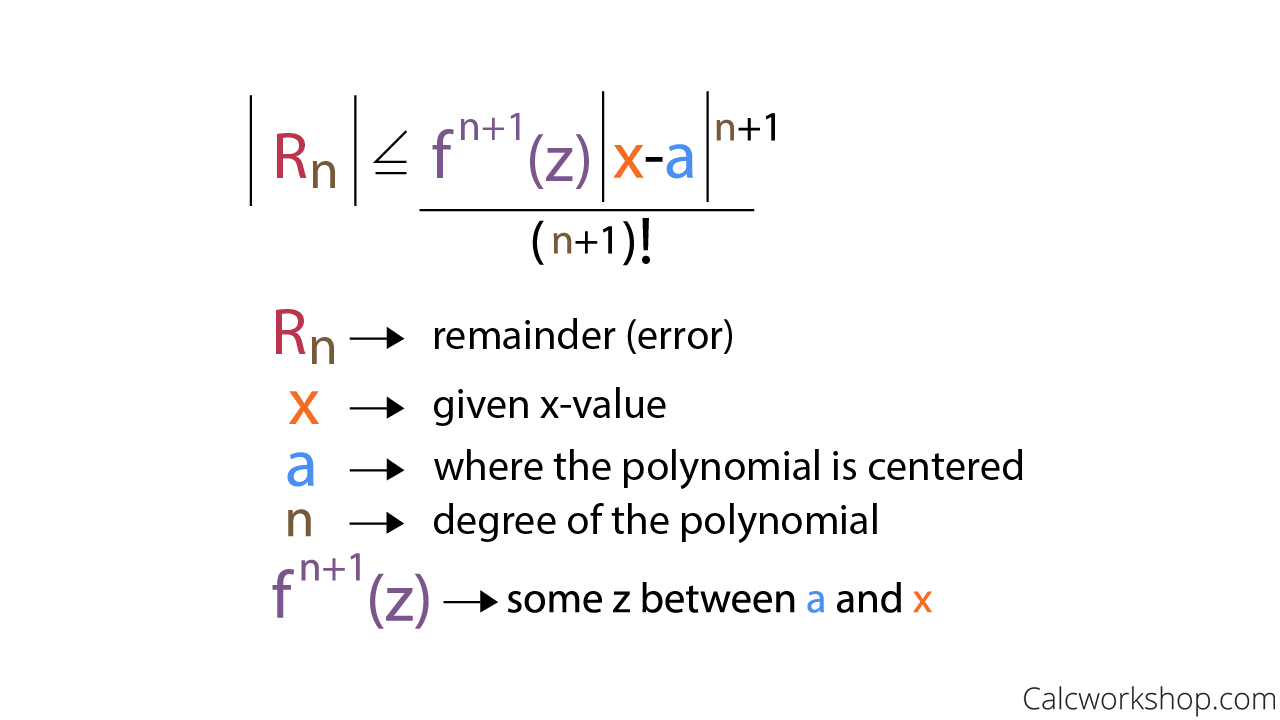
Post a Comment for "taylor series error calculator"